Lorenz-Mie theory : Even though the so-called “Mie” theory began more than 100 years ago with the seminal works of (Lorenz-1890, Mie-1908, and Debye-1909), it continues to be an important source of physical insights and calculational methods).
The “Mie” theory provides an expression for the scattering of light by a homogeneous sphere or radius R, and its importance stems from the fact that it is one of the few exact solutions of a three-dimensional scattering problem. This “exact” solution takes the form of an infinite series of “coefficients”, an and bn, with the integer index n varying from 1 to infinity. These coefficients have analytical expressions that are readily calculated on a computer, and the Mie series converges rapidly for values of n>2πR. A variety of analytical formulas can relate these an and bn coefficients to measurable quantities like the differential and total scattering cross sections, optical forces, modifications to electromagnetic density of states and much more.
Generalized Mie theory and T, S and K-matrices : Historically, our group has contributed to the generalizations of Mie theory to particles other than homogenous spheres, as well as the generalization of the scattering by a single particle to multiple-scattering in multiple-particle systems. This work has typically been carried out principally using the T-matrix formalism (originally developed for quantum mechanics), but some of our recent works have emphasized the utility of the S-matrix and reaction (K) matrix formalisms, also originally developed in the context of quantum and field theoretic scattering. These formulations have also allowed us to describe the interaction of particles with different types of `exotic’ beams like photonic jets and Bessel-type beams. We have carried out several works studying the spectral properties and power transmission of such beams as well as their applications like optical forces.
Applications of Mie theory to Decay rate enhancement : One of the specificities of our group has been to generalize Mie theory to the calculation of the modification of the properties of quantum emitters near optical nano-antenna structures within the weak coupling formalism. The essential idea is that an optical nano-antenna near one its “quasi’’-mode resonances will strongly modify the local density of states (LDOS) which in turn can strongly modify the emission rate of quantum emitters (like fluorophores, quantum dots, etc.) via the LDOS contribution to the Fermi Golden Rule formula. Generalizations of this technique to strongly coupled systems where the properties of the quantum emitter can no longer be considered as being relatively ‘’separate’’ from those of the nano-antennas are currently underway.
Attaining the fundamental limits of light-particle interactions : Certain of our recent works have involved using the S-matrix formalism to establish the fundamental theoretical limits of light-matter interactions, like the unitary limit and ideal absorption (IA) limits. In particular, we have used Weierstrass factorization techniques of S-matrices to make theoretical analytic predictions of the particle properties necessary to reach the unitary or IA limits in a given mode at a given particle size.
(The unitary limit occurs when a given multipole order of a particle reaches its maximal allowed contribution to the extinction(scattering) cross section. For sub-wavelength particles, this corresponds to a large concentration of electromagnetic field energy in the neighborhood of the particle. For dipole interactions this corresponds to a cross section of /2. Ideal absorption corresponds to a particle that attains its maximal allowed absorption cross section (/8 for dipole modes). The concept of IA should prove useful for applications such as solar harvesting and detection.
As an example, we illustrate log scale plots of the electric and magnetic near-field intensities near particles that were designed to achieve Ideal Absorption (IA) in electric and magnetic dipole modes respectively when kR=0.4. The fields exterior to the particles have identical profiles, but the magnetic IA particles have much stronger fields inside the particle.
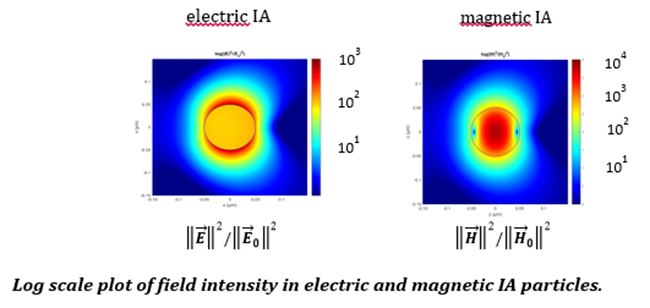
Studies currently underway in our group include evaluate the means of concentrating electromagnetic energy inside particles for applications in non-linear and quantum optics. This work is being carried out by reinforcing our design methods using Weierstrass factorization and coupled quasi-mode analysis.


 ResearchGate
ResearchGate Flux RSS
Flux RSS