Institut Fresnel

Les nouvelles structures photoniques résonantes sont modélisées par des paramètres homogènes effectifs (voir paragraphe précédent) qui sont par nature dispersifs, c’est-à-dire dépendant de la fréquence.
Parallèlement à ces modèles, des recherches ont été engagées à l’Institut Fresnel pour comprendre les effets de ce phénomène de dispersion dans les nouveaux composants.
Ces recherches reposent sur des connaissances sans équivalent au niveau international, depuis qu’a été établi un cadre étendu des équations de Maxwell pour les métamatériaux [J. Math. Phys. 51, 052902 (2010)], qui permet de « simplifier » la dispersion et l’absorption (en collaboration avec AMOLF, FOM-Institute, Amsterdam).

Ce cadre étendu a été appliqué à la lentille parfaite d’indice négatif pour établir une formulation bien posée du problème et pour montrer rigoureusement les limites de la résolution infinie en régime temporel [Gra-3].
En lien avec l’homogénéisation hautes fréquences, ce cadre a été utilisé pour établir une preuve rigoureuse des propriétés de causalité, de passivité et de comportement asymptotique aux hautes fréquences pour les paramètres effectifs des multicouches [Liu-2].
Ces nouvelles connaissances permettent aussi de revisiter la problématique ancienne de la propagation du champ électromagnétique dans les milieux dispersifs dans de nouveaux contextes : dans la lentille plate d’indice négatif [Gra-3] et dans des systèmes invisibles conçus à partir de l’optique de transformation, avec la mise en évidence théorique d’analogues des précurseurs de Brillouin [Gra-1]. Enfin, une version spatio-temporelle des relations de Kramers-Kronig, étendue au vecteur d’onde, a été utilisée pour proposer une nouvelle technique de reconstruction de la phase à partir de l’intensité [Gra-2].
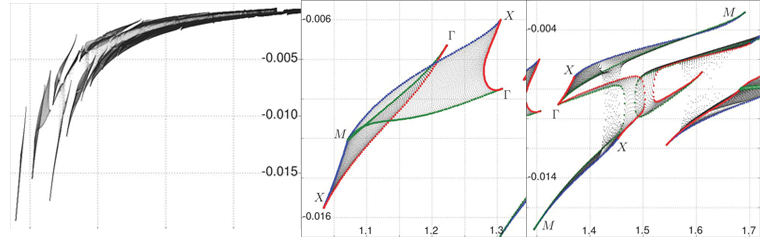
Ces nouvelles connaissances sont aussi exploitées pour augmenter les possibilités des codes numériques. Le cadre étendu des équations de Maxwell a été implémenté dans la méthode des éléments finis pour calculer de façon très efficace les relations de dispersion des cristaux photoniques 2D avec dispersion et absorption [Bru-1] (figure 1.3). Ce transfert de connaissances théoriques vers les méthodes numériques est le point de départ du calcul des modes quasi normaux dans les systèmes dispersifs (voir Méthode des éléments finis).

[Liu-2] Yan Liu, Sébastien Guenneau, Boris Gralak. Causality and passivity properties of effective parameters of electromagnetic multilayered structures. Physical Review B, 2013, 88, pp.165104.
[Gra-1] Boris Gralak, Arismendi Genaro, Sébastien Guenneau, Avril Benoît, André Diatta. Analysis in temporal regime of dispersive invisible structures designed from transformation optics. Physical Review B, 2016, 93, pp.121114(R).
[Gra-2] Boris Gralak, Michel Lequime, Myriam Zerrad, Claude Amra. Phase retrieval of reflection and transmission coefficients from Kramers–Kronig relations. Journal of the Optical Society of America A, 2015, 32, pp.000456.
[Gra-3] Boris Gralak, Daniel Maystre. Negative index materials and time-harmonic electromagnetic field. Comptes Rendus Physique, 2012, 13, pp.786.
[Bru-1] Yoann Brûlé, Boris Gralak, Guillaume Demésy. Calculation and analysis of the complex band structure of dispersive and dissipative two-dimensional photonic crystals. Journal of the Optical Society of America B, 2016, 33, pp.691.