Etude des modes de fibres optiques microstructurées à
section arbitraire à l'aide de la nouvelle méthode
différentielle « Fast Fourier Factorization »
Philippe Boyer, Gilles Renversez, Evguéni Popov, Michel Nevière
Institut Fresnel, Case 161, Unité Mixte de Recherche Associée au Centre National de la Recherche Scientifique
(UMR 6133), Université Paul Cézanne Aix-Marseille III, Université de Provence, Faculté des Sciences et
Techniques de St. Jérôme, Avenue Escadrille Normandie Niémen, 13397 Marseille Cedex 20, France
Tél : (33)4.91.28.88.24, Fax : (33)4.91.67.44.28, e-mail: philippe.boyer@fresnel.fr
Les fibres optiques microstructurées (MOFs) présentent
un intérêt croissant dans la communauté scientifique depuis une
décennie environ. En effet, l'accroissement des puissances des
calculateurs permettent d'envisager l'application de nouvelles
méthodes numériques afin de prévoir et de limiter les
phénomènes de dispersion et de pertes au sein de nouvelles
structures de fibres optiques. La méthode multipolaire (MM) [1]
développée et étudiée dans notre laboratoire, a déjà fournit de
nombreux résultats sur la physique des MOFs. Toutefois cette
méthode rigoureuse et rapide possède les limitations suivantes :
Elle peut considérer uniquement des inclusions inscrites dans des
cercles disjoints et la matrice doit garder un indice constant. Afin
de modéliser de nouvelles MOFs à sections arbitraires et/ou
contenant des milieux inhomogènes, nous sommes ainsi amener à
considérer de nouvelles méthodes numériques.
Notre choix s'est naturellement orienté sur une méthode
différentielle récemment mise au point dans le laboratoire et
appelée : « Fast Fourier Factorization » (FFF) [2]. Après avoir été
appliquée avec succès au cas de la diffraction de la lumière par
des objets cylindriques à sections arbitraires, nous cherchons à
l'adapter à la recherche de modes dans les MOFs. Le principe de la FFF est d'obtenir une nouvelle formulation
des équations de Maxwell dans un espace de Fourier tronqué (développement de Fourier des grandeurs
optogéométriques) en appliquant de nouvelles règles de factorisation dans les relations constitutives des milieux.
Ainsi, la troncature des développements en vue d'une application numérique, mais aussi les discontinuités de
certaines grandeurs optogéométriques (relations de continuité des champs, discontinuité des indices à travers les
surfaces) sont pris en compte et assurent une convergence plus rapide que la méthode différentielle classique.
Les calculs numériques aboutissent à une matrice de transmission (matrice T) intrinsèque à la géométrie du
système mais présentant certaines instabilités numériques dues à des contaminations lors du processus
d'intégration des équations de Maxwell (système différentiel des coefficients de Fourier des champs selon la
variable radiale r). Ces problèmes sont corrigés grâce à l'utilisation de l' « algorithme de propagation S »
aboutissant à l'obtention de la matrice S. Les développements des champs associés aux modes deviennent alors
les solutions du problème homogène dont le système
d'équations linéaires a pour matrice : S
-1
. Par conséquent, nous
cherchons l'indice effectif qui annule le déterminant de cette
dernière matrice ; et les champs sont décrits par les vecteurs
propres associés aux valeurs propres nulles de la matrice S
-1
évaluée aux indices effectifs trouvés auparavant. De plus, la
sous-périodicité selon la coordonnée polaire
du système,
caractéristique des MOFs couramment étudiées (voir Figure
1), implique un découplage du système différentiel à intégrer
en autant de sous-systèmes que l'ordre de la périodicité. Très
récemment, la sous-périodicité en
fut implémenté dans le
code permettant de réduire de manière très significative le
temps de calculs.
La validation de la méthode FFF appliquée aux
MOFs est obtenue par comparaison avec la MM et pour un
fibre optique dont la section droite est constituée de 6
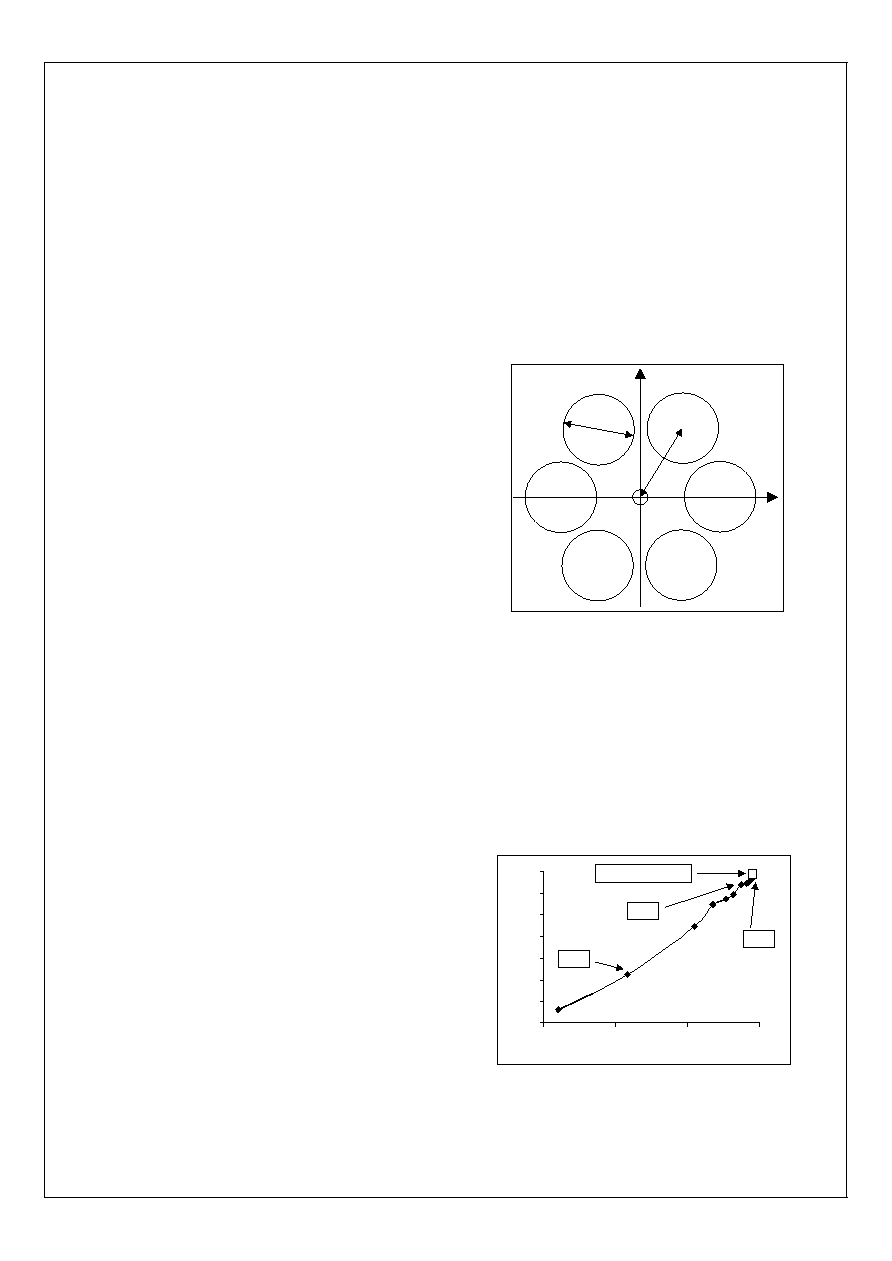
Figure. 1. Section droite d'une MOF à 6 inclusions
circulaires avec d = 1
µm, = 2.3 µm, n
int
= 1 et
n
ext
= 1.4439, et notations.
0
y
x
n
ext
z
n
int
n
int
n
int
n
int
n
int
n
int
d
7.175
7.180
7.185
7.190
7.195
7.200
7.205
7.210
1.420770
1.420775
1.420780
1.420785
Figure. 2. Test de convergence de l'indice effectif du
mode fondamental selon l'ordre maximal des
développements de Fourier N.
N=30
N=60
N=90
Re(n
eff
)
Im(n
eff
) Multipole Method
16

