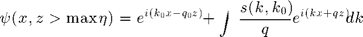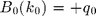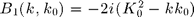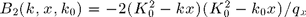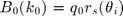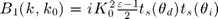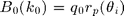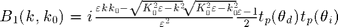The Small Perturbation Method for 2D scattering from Gaussian random rough surface
Contents
- The scattering amplitude
- The perturbative expansion
- The Dirichlet boundary condition
- The Neumann boundary condition
- The transmission problem for S-polarized electromagnetic waves
- The transmission problem for P-polarized electromagnetic waves
- Stationary random rough surface with normal height distribution and Gaussian roughness spectrum
- *** THE COHERENT REFLEXION COEFFICIENT ***
- The Dirichlet boundary condition
- The incoherent bistatic coefficient
- *** THE DIFFERENTIAL REFLECTIVITY ***
- Monostatic diagrams
- Bistatic diagrams
- Summary - 2D scattering
The scattering amplitude
For an incident plane wave impinging from air a 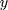 -invariant surface
-invariant surface 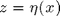 with an angle
with an angle 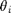 from the
from the  -axis, the field in the air above the surface region (that is
-axis, the field in the air above the surface region (that is 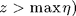 writes as the plane wave sum :
writes as the plane wave sum : 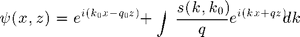 for an implicit
for an implicit 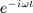 time dependency. With wavenumber
time dependency. With wavenumber 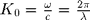 ,
, 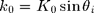 and
and 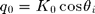 define the incident wavevector. For the scattering one,
define the incident wavevector. For the scattering one, 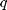 is chosen so that
is chosen so that 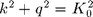 with
with 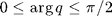 .
.
lambda=1; % the EM wavelength is chosen as length unit K0=2*pi/lambda; qf=@(k,ep) sqrt(K0^2*ep-k.^2); % ep=1 in air
The perturbative expansion
Assuming 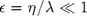 and following the small perturbation method (SPM), the scattering amplitude
and following the small perturbation method (SPM), the scattering amplitude 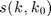 is expanded into a series :
is expanded into a series : 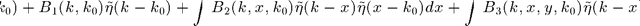 where
where 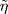 is the Fourier transform of the height function
is the Fourier transform of the height function 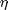
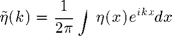 and the coefficients
and the coefficients 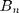 are roughness-independent.
are roughness-independent.
The Dirichlet boundary condition
Enforcing 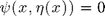 on the surface leads to :
on the surface leads to :
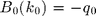
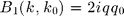
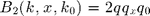 with
with 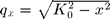
BD0=@(k0) -qf(k0,1); BD1=@(k,k0) 2*1i*qf(k,1).*qf(k0,1); BD2=@(k,x,k0) 2*qf(k,1).*qf(x,1).*qf(k0,1);
The Neumann boundary condition
Enforcing 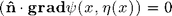 on the surface leads to :
on the surface leads to :
BN0=@(k0) +qf(k0,1); BN1=@(k,k0) -2*1i*(K0^2-k.*k0); BN2=@(k,x,k0) -2*(K0^2-k.*x).*(K0^2-k0.*x)./qf(x,1);
The transmission problem for S-polarized electromagnetic waves
Assuming continuity of both the field 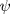 and its normal derivative
and its normal derivative 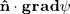 when passing from air (wavenumber K_0) to the scattering medium (wavenumber
when passing from air (wavenumber K_0) to the scattering medium (wavenumber 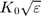 ), we first define reflection
), we first define reflection 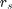 coefficient for the plane :
coefficient for the plane : 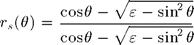 and associated transmission coefficient
and associated transmission coefficient 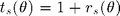 . Then,
. Then,
This corresponds to the transmission problem of an electromagnetic wave which electric field is parallel to the invariance direction 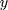 , between air and a nonmagnetic medium of relative permittivity
, between air and a nonmagnetic medium of relative permittivity  .
.
rs=@(k,ep) (qf(k,1)-qf(k,ep))./(qf(k,1)+qf(k,ep)); ts=@(k,ep) 1+rs(k,ep); BS0=@(k0,ep) +qf(k0,1).*rs(k0,ep); BS1=@(k,k0,ep) 0.5*1i*K0^2*(ep-1).*ts(k,ep).*ts(k0,ep);
The transmission problem for P-polarized electromagnetic waves
Now considering an electromagnetic wave wich electric field is in the incidence plane, that is perpendicular to the invariance direction 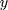 , it is the quantity
, it is the quantity 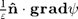 that is continuous besides filed
that is continuous besides filed 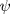 . When passing from air (wavenumber K_0) to the scattering medium (wavenumber
. When passing from air (wavenumber K_0) to the scattering medium (wavenumber 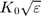 ), we first define reflection
), we first define reflection 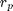 coefficient for the plane :
coefficient for the plane : 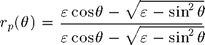 and associated transmission coefficient
and associated transmission coefficient 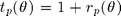 . Then,
. Then,
This corresponds to the transmission problem of an electromagnetic wave which electric field is parallel to the invariance direction 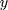 , between air and a nonmagnetic medium of relative permittivity
, between air and a nonmagnetic medium of relative permittivity  .
.
rp=@(k,ep) (ep*qf(k,1)-qf(k,ep))./(ep*qf(k,1)+qf(k,ep)); tp=@(k,ep) 1+rp(k,ep); BP0=@(k0,ep) +qf(k0,1).*rp(k0,ep); BP1=@(k,k0,ep) 0.5*1i*((ep-1)*(ep*k.*k0-qf(k,ep).*qf(k0,ep))/ep^2).*tp(k,ep).*tp(k0,ep);
Stationary random rough surface with normal height distribution and Gaussian roughness spectrum
The surface 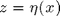 is a stationary centered random process with normally-distributed height. The roughess spectrum
is a stationary centered random process with normally-distributed height. The roughess spectrum 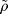 , Fourier transform of the two-points correlation function
, Fourier transform of the two-points correlation function 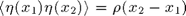 , with brackets denoting statistical averaging, is a Gaussian function with two parameters
, with brackets denoting statistical averaging, is a Gaussian function with two parameters 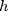 and
and  the height root mean quare and correlation length, respectively.
the height root mean quare and correlation length, respectively. 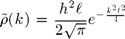
h=lambda/50; l=lambda/2; spec=@(k) (0.5*h^2*l/sqrt(pi))*exp(-0.25*k.^2*l^2);
*** THE COHERENT REFLEXION COEFFICIENT ***
Stationarity implies that the mean field writes in air above the surface region : 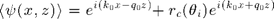 as the sum of the incident field and a specularly-reflected plane wave. The amplitude of that reflection defines the coherent reflexion coefficient. It is related to the scattering amplitude by :
as the sum of the incident field and a specularly-reflected plane wave. The amplitude of that reflection defines the coherent reflexion coefficient. It is related to the scattering amplitude by : 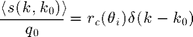 in the general case, and applying the third-order SPM expansion to Gaussian process,
in the general case, and applying the third-order SPM expansion to Gaussian process, 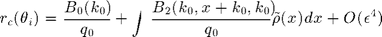 since, due to the Gaussian moment theorem, first- and third-orders do not contribute.
since, due to the Gaussian moment theorem, first- and third-orders do not contribute.
xmax=6*(sqrt(2)/l); % integration bound for Gaussian spectrum
rc=@(k0,B0,B2) B0(k0)./qf(k0,1)+integral(@(x)B2(k0,k0+x,k0).*spec(x)./qf(k0,1),-xmax,xmax);
The Dirichlet boundary condition
tid=[0:35 37:89]; for ii=1:length(tid) spm2rcd(ii)=rc(K0*sind(tid(ii)),BD0,BD2); spm2rcn(ii)=rc(K0*sind(tid(ii)),BN0,BN2); end figure(1) subplot(121) [AX,H1,H2]=plotyy(tid,abs(spm2rcd),tid,angle(spm2rcd)*180/pi);grid on set(AX(1),'FontSize',24,'XLim',[0 90],'XTick',[0:15:90]) set(AX(2),'FontSize',24,'XLim',[0 90],'XTick',[0:15:90]) set(H1,'LineWidth',2) set(H2,'LineWidth',2) xlabel('Incidence angle (deg)') title('Coherent reflexion coefficient - Dirichlet') subplot(122) [AX,H1,H2]=plotyy(tid,abs(spm2rcn),tid,angle(spm2rcn)*180/pi);grid on set(AX(1),'FontSize',24,'XLim',[0 90],'XTick',[0:15:90]) set(AX(2),'FontSize',24,'XLim',[0 90],'XTick',[0:15:90]) set(H1,'LineWidth',2) set(H2,'LineWidth',2) xlabel('Incidence angle (deg)') title('Coherent reflexion coefficient - Neumann') legend('Modulus','Argument (deg)','Location','Best')
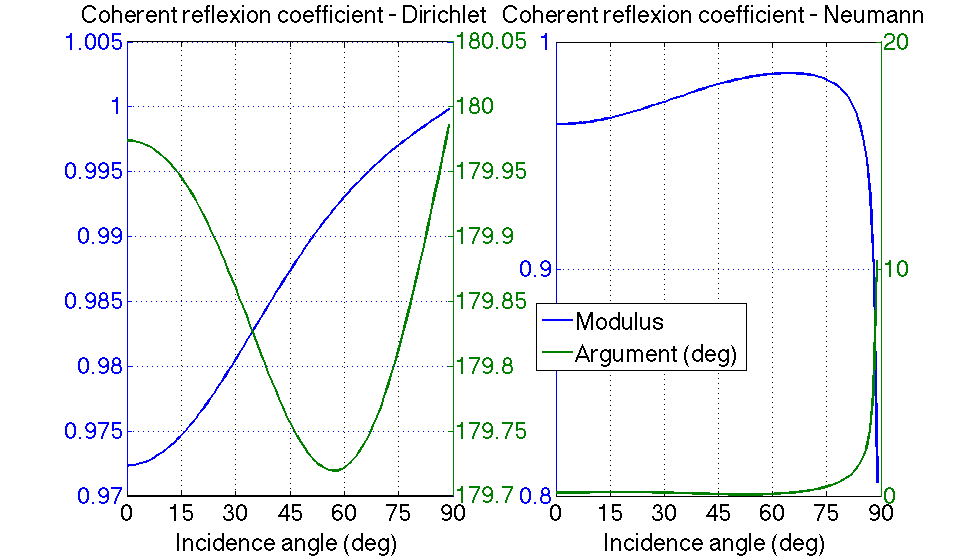
The incoherent bistatic coefficient
With 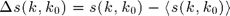 the incoherent scattered amplitude, the incoherent bistatic coefficent
the incoherent scattered amplitude, the incoherent bistatic coefficent 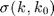 is defined by
is defined by 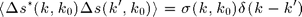 For a Gaussian process, the SPM expansion leads to :
For a Gaussian process, the SPM expansion leads to : 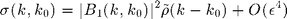 since, due to the Gaussian moment theorem, the third-order contribution vanishes.
since, due to the Gaussian moment theorem, the third-order contribution vanishes.
*** THE DIFFERENTIAL REFLECTIVITY ***
In air, the time-averaged power density through an horizontal plane is proportional to 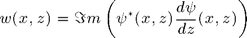 It writes
It writes 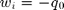 for the incident plane wave and
for the incident plane wave and 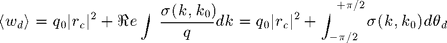 for the statistically averaged scattered field. Note that only the propagative part of the scattered field contributes. The reflectivity
for the statistically averaged scattered field. Note that only the propagative part of the scattered field contributes. The reflectivity 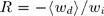 thus writes :
thus writes : 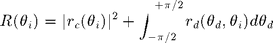 introducing
introducing 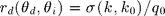 the (incoherent) differential reflectivity :
the (incoherent) differential reflectivity : 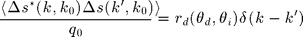
rd=@(k,k0,B1) abs(B1(k,k0)).^2.*spec(k-k0)./qf(k0,1);
Monostatic diagrams
tid=[0:89]; k0=K0*sind(tid); k=-k0; % backscattering configuration spm1rdd=rd(k,k0,BD1); % Dirichlet spm1rdn=rd(k,k0,BN1); % Neumann ep=2.25; % dielectric constant of glass at optical frequencies spm1rds=rd(k,k0,@(k,k0)BS1(k,k0,ep)); % S-pol. spm1rdp=rd(k,k0,@(k,k0)BP1(k,k0,ep)); % P-pol. dB=@(x) 10*log10(x); figure(2) H1=plot(tid,dB(spm1rdd),tid,dB(spm1rdn),tid,dB(spm1rds),tid,dB(spm1rdp));grid on set(gca,'FontSize',24,'XLim',[0 90],'XTick',[0:15:90]) set(H1,'LineWidth',2) xlabel('Monostatic angle (deg)') title('Differential reflectivity - dB') legend('Dirichlet','Neumann','S-pol.','P-pol.','Location','Best')
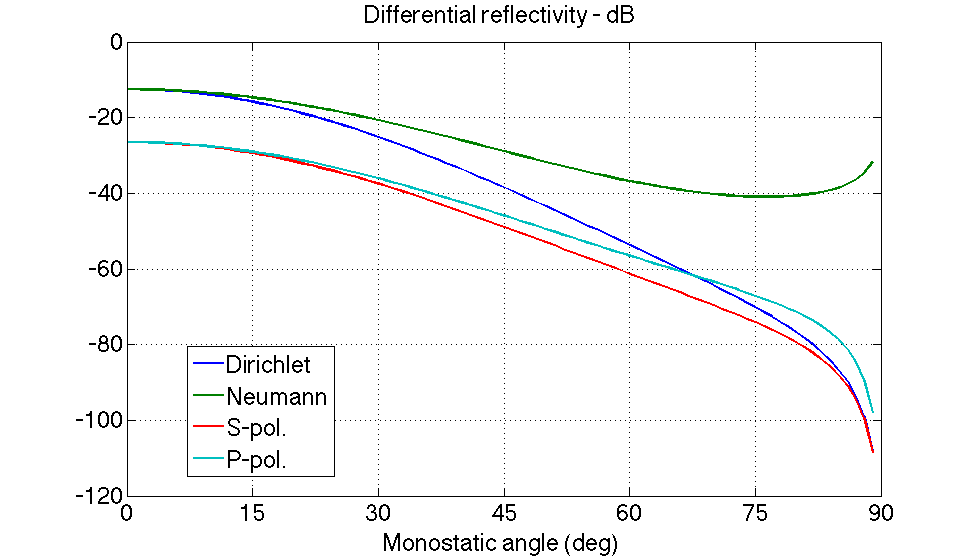
Bistatic diagrams
ep=2.25; % dielectric constant of glass at optical frequencies tid=atand(sqrt(ep)); % The BREWSTER angle fprintf('The Brewster angle is %gdeg for index %g\n',tid,sqrt(ep)) k0=K0*sind(tid); tsd=[-89:89]; k =K0*sind(tsd); spm1rdd=rd(k,k0,BD1); % Dirichlet spm1rdn=rd(k,k0,BN1); % Neumann spm1rds=rd(k,k0,@(k,k0)BS1(k,k0,ep)); % S-pol. spm1rdp=rd(k,k0,@(k,k0)BP1(k,k0,ep)); % P-pol. dB=@(x) 10*log10(x); figure(3) H1=plot(tsd,dB(spm1rdd),tsd,dB(spm1rdn),tsd,dB(spm1rds),tsd,dB(spm1rdp));grid on set(gca,'FontSize',24,'XLim',[-90 90],'XTick',[-90:15:90]) set(H1,'LineWidth',2) xlabel('Scattering angle (deg)') title('Differential reflectivity - dB') legend('Dirichlet','Neumann','S-pol.','P-pol.','Location','Best')
The Brewster angle is 56.3099deg for index 1.5
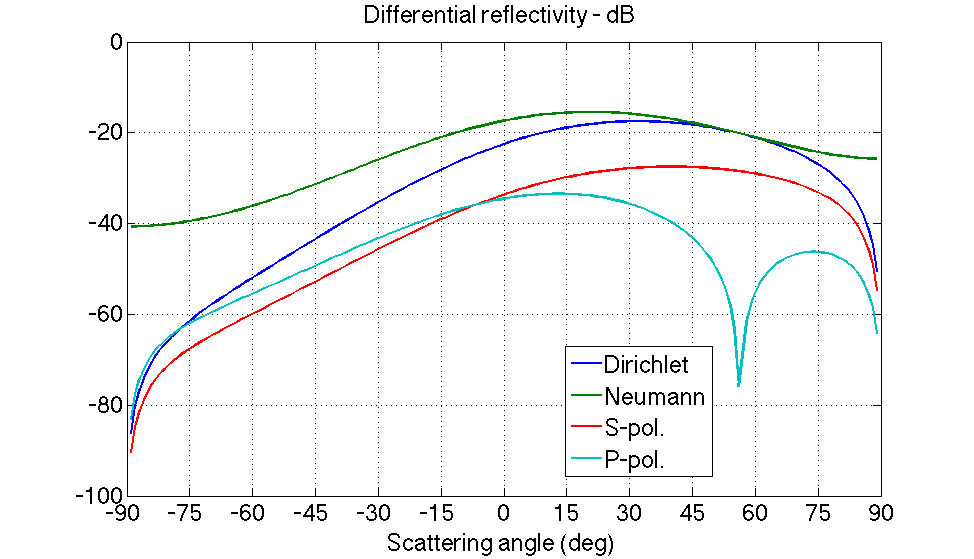
Summary - 2D scattering
The rough surface reflectivity decomposes as 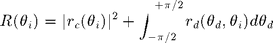 with
with 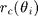 the coherent reflexion coefficient
the coherent reflexion coefficient 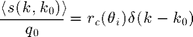 and
and 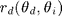 the (incoherent) differential reflectivity
the (incoherent) differential reflectivity 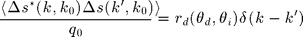 both obtained from the scattering amplitude
both obtained from the scattering amplitude 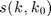 , itself defined through
, itself defined through